| > | restart; |
| > | libname := libname,"d:/Tomas/ČVUT/B071/x31das/semestrálka/PraCAn"; |
Návrh SC pásmové propusti Chebyshev metodou funkční simulace,
fclock = 10 kHz, fm = 1 kHz, deltafp = 1 kHz, deltafs = 2 kHz, ap = 1 dB, as = 30 dB.
Sepsal l. P. 2008 Bc. Tomáš Bořil.
Na motivy metody "porovnávání jmenovatelů přenosových funkcí"
z knihy 'Switched Capacitor Filters - Theory, Analysis and Design'
by
B. Ramachandran - etc. - P.V. Anandamohan - M.N.S. Swamy.
Autor byl inspirován převážně příkladem 7.1 (Design an LDI-type LP ladder filter) z kapitoly 7.1.2,
dále pak kapitolou 7.4.2 (SC band-pass ladder filters based on LDI transformation).
Všechna práva vyhrazena, během semestrální práce nebylo ublíženo žádnému zvířeti.
| > |
Spinací perioda
| > | T := 1 / 10e3; |
![[Maple Metafile]](images/pp53.gif)
Prewarpování jednotlivých frekvencí (podle vztahu dole na str. 149)
Jednotlivé frekvence jsme získali pomocí Syntfilu zadáním našich "delta" frekvencí.
| > | prewarp := fpuvodni -> 2/T * sin(2*Pi*fpuvodni * T/2) / (2*Pi); |
| > | f_s := evalf(prewarp(414.214)); |
| > | f_p := evalf(prewarp(618.034)); |
| > | fp := evalf(prewarp(1.618e3)); |
| > | fs := evalf(prewarp(2.414e3)); |
| > |
Zadali jsme nové frekvence do Syntfilu a získali tak přenosovou funkci
| > | H := p -> (292411879405405*p^4)/(p^8 + 5596.60968212060*p^7 + 200390505.539602*p^6 + 781070617011.267*p^5 + .125591755560536e17*p^4 + .293346944014671e20*p^3 + .282656955267829e24*p^2 + .296482335350600e27*p + .198959678828995e31); |
| > |
Přenos analogového prototypu
| > | plot(20*log10(abs(eval(H(p), p = I*2*Pi*f))), f = 0..5000); |
![[Maple Plot]](images/pp511.gif)
| > |
Struktura RLC (získaná ze Syntfilu)
![[Maple Metafile]](images/pp512.gif)
| > |
Funkční simulace - popis obvodovými rovnicemi
![[Maple Metafile]](images/pp513.gif)
| > |
Z rovnic sestavený obvod
![[Maple Metafile]](images/pp514.gif)
| > |
Úprava, aby vstupy do sumátorů byly kladné
![[Maple Metafile]](images/pp515.gif)
| > |
Převrácení vzhůru nohama z důvodu názornější korespondence s následující SC realizací
![[Maple Metafile]](images/pp516.gif)
| > |
Výsledná SC realizace pomocí bezeztrátových a ztrátových integrátorů. Nakonec jsme se z důvodu následující metody "porovnávání koeficientů přenosových funkcí" (viz příklad 7.1 v kapitole 7.1.2 knihy uvedené v literatuře) pro hledání hodnot součástek rozhodli funkční simulaci roztrhnout na dvě sekce čtvrtých řádů (viz kapitola 7.4.2) zapojené do kaskády, protože řešit soustavu osmi nelineárních rovnic o osmi neznámých by bylo náročné.
Všimněme si, že oproti původní struktuře není v sekci 1 použit zatěžovací kapacitor CL a naopak v sekci 2 není použit vstupní kapacitor CS.
Vstup obvodu je v uzlu 1, výstup první sekce v uzlu 6 a výstup celé kaskády filtru v uzlu 26. Jak je dále ukázáno, šipkou označené kapacitory hrají zásadní roli pro nastavení zesílení jednotlivých sekcí.
Tužkou jsou naznačeny skutečné názvy součástek, propiskou čísla uzlů.
![[Maple Metafile]](images/pp517.gif)
| > |
Tímto jsme odvodili výslednou SC strukturu filtru. Nyní přistupme k LDI (loseless discrete integrator) transformaci původní analogové přenosové funkce (získané z prewarpovaného tolerančního schematu pomocí Syntfilu), analýze spinaného obvodu a hledání hodnot součástek porovnáváním koeficientů transformované přenosové funkce s přenosovou funkcí navrženého SC obvodu.
| > |
Postup transformace: najdeme nuly a póly analogové funkce, ty přetransformujeme do z-roviny a z nich pak sestavíme novou transformovanou přenosovou funkci.
| > |
LDI Transformace čitatele - jen pro dobrý pocit, pro náš algoritmus návrhu není potřeba, jelikož budeme porovnávat pouze koeficienty jmenovatelů.
| > | numer(H(p)); |
| > | solve(numer(H(p)) = 0); |
| > | nuly := 1 + 0*T * (0*T/2 + sqrt(0^2 * T^2 + 4) / 2); |
| > | citatel := coeff(numer(H(p)), p, 4) * expand((z-1)*(z-1)*(z-1)*(z-1)); |
| > |
LDI transformace jmenovatele
| > | poly := solve(denom(H(p)) = 0); |
| > |
Póly jsme se rozhodli z důvodu přesnosti přepsat přímo ze Syntfilu.
| > | polyP[1] := -1181.22950453796-7364.43571690615*I: polyP[2] := -1181.22950453796+7364.43571690615*I: polyP[3] := -797.470824402930-4971.87261227509*I: polyP[4] := -797.470824402930+4971.87261227509*I: polyP[5] := -584.761573663095-9652.74516722974*I: polyP[6] := -584.761573663095+9652.74516722974*I: polyP[7] := -234.842938456321-3876.58687119603*I: polyP[8] := -234.842938456321+3876.58687119603*I: |
| > |
Transformace pólů z p-roviny do z-roviny, před sqrt() je buď plus nebo mínus, o znaménku rozhodujeme tak, aby výsledek ležel uvnitř jednotkové kružnice z-roviny.
| > | for iiii from 1 to 8 do polyZ[iiii] := 1 + polyP[iiii]*T * (polyP[iiii]*T/2 + sqrt(polyP[iiii]^2 * T^2 + 4) / 2); abs(polyZ[iiii]); end do; |
![polyZ[1] := .6429089480-.6020606465*I](images/pp524.gif){kind=small}
![polyZ[2] := .6429089480+.6020606465*I](images/pp526.gif){kind=small}
![polyZ[3] := .8073522472-.4431803032*I](images/pp528.gif){kind=small}
![polyZ[4] := .8073522472+.4431803032*I](images/pp530.gif){kind=small}
![polyZ[5] := .5001219037-.7905167295*I](images/pp532.gif){kind=small}
![polyZ[6] := .5001219037+.7905167295*I](images/pp534.gif){kind=small}
![polyZ[7] := .9029947818-.3712857337*I](images/pp536.gif){kind=small}
![polyZ[8] := .9029947818+.3712857337*I](images/pp538.gif){kind=small}
Kompletní transformovaná přenosová funkce
Pozor na roznásobování, kdybychom neprovedli vnitřní funkce expand pro každá dvě komplexně sdružená čísla, ale pouze jedno vnější expand, dostali bychom kvůli nepřesnostem floating-point výpočtů jiný výsledek (nesmyslné imaginární členy)!
| > | spatneHd := citatel / expand( (z-polyZ[1])*(z-polyZ[2]) * (z-polyZ[3])*(z-polyZ[4]) * (z-polyZ[5])*(z-polyZ[6]) * (z-polyZ[7])*(z-polyZ[8]) ); |
| > |
| > | Hd := citatel / expand( expand((z-polyZ[1])*(z-polyZ[2])) * expand((z-polyZ[3])*(z-polyZ[4])) * expand((z-polyZ[5])*(z-polyZ[6])) * expand((z-polyZ[7])*(z-polyZ[8])) ); |
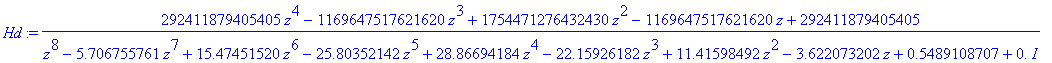
Umazání 0*I ze jmenovatele
| > | Hd := evalc(Re(Hd)); |
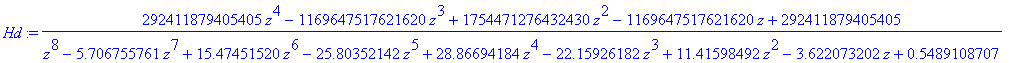
Jmenovatel přenosu
| > | Hdd := denom(Hd); |
Rozklad, kvůli obvodové realizaci totiž potřebujeme získat 2 sekce
| > | factor(Hdd); |
1. část jmenovatele (použijeme v 1. sekci obvodu)
| > | Hdd1 := collect((z^2-1.000243833*z+.8750386484)*(z^2-1.285817665*z+.7758087625), z); |
Dělíme koeficientem u členu z^0 tak, aby ve jmenovateli byl poslední člen 1.
| > | c1 := coeff(Hdd1, z, 0); |
| > | Hdd1 := Hdd1 / c1; |
2. část jmenovatele (použijeme v 2. sekci obvodu)
| > | Hdd2 := collect((z^2-1.614705158*z+.8482269248)*(z^2-1.805989105*z+.9532523004), z); |
Dělíme koeficientem u členu z^0 tak, aby ve jmenovateli byl poslední člen 1.
| > | c2 := coeff(Hdd2, z, 0); |
| > | Hdd2 := Hdd2 / c2; |
| > |
Konečný tvar čitatele (pro algoritmus není potřeba)
| > | Hdnfactor := factor(numer(Hd)) / c1 / c2; |
| > |
| > | ####### |
Vyšetřování přenosu 1. sekce obvodu (bez zadaných hodnot kapacit)
| > |
Analýzami obvodu se nám podařilo zjistit, že funkce obvodu nezávisí na zvolených hodnotách Cs a Cl, protože hodnoty ostatních kapacitor; jsou z těchto hodnot vypočítávány a výsledná přenosová funkce je pak vždy nakonec shodná. Proto jsme se rozhodli Cs a Cl zvolit stejně jako Cu jednotkové.
| > |
| > | obvpp:=" |
| > | V1 1 0 1 AC S1 2 1 1 S2 2 4 2 S3 3 0 1 S4 3 5 2 S5 8 0 1 S6 8 6 2 S7 9 0 1 S8 9 5 2 S9 10 0 1 S10 10 5 2 S11 11 0 1 S12 11 7 2 S13 13 12 1 S14 13 0 2 S15 14 0 1 S16 14 7 2 S17 16 15 1 S18 16 0 2 S19 17 18 1 S20 17 7 2 S21 19 6 1 S22 19 0 2 S23 20 0 1 S24 20 21 2 S25 22 6 1 S26 22 24 2 S27 23 0 1 S28 23 25 2 S29 27 0 1 S30 27 26 2 S31 28 0 1 S32 28 25 2 S33 31 30 1 S34 31 0 2 S35 32 0 1 S36 32 29 2 S37 34 33 1 S38 34 0 2 S39 35 36 1 S40 35 29 2 S41 37 26 1 S42 37 0 2 S43 38 33 1 S44 38 0 2 S45 39 26 1 S46 39 0 2 S47 40 0 1 S48 40 41 2 A1 7 0 0 5 A2 4 0 0 12 A3 6 0 0 15 A4 18 0 0 21 A5 29 0 0 25 A6 24 0 0 30 A7 26 0 0 33 A8 36 0 0 41 Cu1 2 3 1 Cu2 8 9 1 Cu3 13 14 1 Cu4 16 17 1 Cu5 19 20 1 Cs 10 11 1 Cc1 5 7 Cl1 4 12 Cl2 6 15 Cc2 21 18 Cu6 22 23 1 Cu7 27 28 1 Cu8 31 32 1 Cu9 34 35 1 Cu10 39 40 1 Cl 37 38 1 Cc3 25 29 Cl3 24 30 Cl4 26 33 Cc4 41 36 .end": |
| > |
| > | vysledky := PraCAn(obvpp, TF, P = 2, SCIDEAL): prenos := eval(v("6")[1] / v("1")[1], vysledky); |
| > |
Jmenovatel přenosu
| > | collect(denom(prenos), z); |
| > |
Dělíme koeficientem členu z^0 tak, aby poslední člen jmenovatele byl 1.
| > | jmenovatel1 := collect(% / coeff(%, z, 0), z); |
| > |
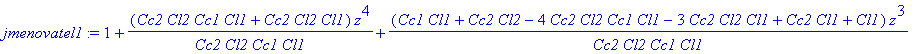
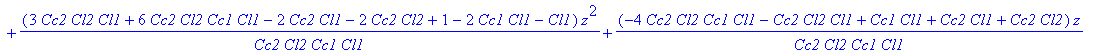
Jmenovatel funkce, kterou chceme touto sekcí realizovat
| > | Hdd1; |
Porovnání koeficientů - nalezení hodnot součástek
| > | hodnoty1 := solve({ coeff(jmenovatel1, z, 4) = coeff(Hdd1, z, 4), coeff(jmenovatel1, z, 3) = coeff(Hdd1, z, 3), coeff(jmenovatel1, z, 2) = coeff(Hdd1, z, 2), coeff(jmenovatel1, z, 1) = coeff(Hdd1, z, 1) }, {Cc1, Cl1, Cl2, Cc2}); |
| > |
Vyšetřování přenosu 2. sekce obvodu (bez zadaných hodnot kapacit)
| > | ### |
| > | obvpp:=" |
| > | V1 6 0 1 AC S25 22 6 1 S26 22 24 2 S27 23 0 1 S28 23 25 2 S29 27 0 1 S30 27 26 2 S31 28 0 1 S32 28 25 2 S33 31 30 1 S34 31 0 2 S35 32 0 1 S36 32 29 2 S37 34 33 1 S38 34 0 2 S39 35 36 1 S40 35 29 2 S41 37 26 1 S42 37 0 2 S43 38 33 1 S44 38 0 2 S45 39 26 1 S46 39 0 2 S47 40 0 1 S48 40 41 2 A5 29 0 0 25 A6 24 0 0 30 A7 26 0 0 33 A8 36 0 0 41 Cu6 22 23 1 Cu7 27 28 1 Cu8 31 32 1 Cu9 34 35 1 Cu10 39 40 1 Cl 37 38 1 Cc3 25 29 Cl3 24 30 Cl4 26 33 Cc4 41 36 .end": |
| > |
| > |
| > | vysledky := PraCAn(obvpp, TF, P = 2, SCIDEAL): |
| > | prenos := eval(v("26")[1] / v("6")[1], vysledky); |
| > |
Jmenovatel přenosu
| > | collect(denom(prenos), z); |
| > |
Dělíme posledním členem jmenovatele (bez z) tak, aby poslední člen jmenovatele byl 1.
| > | jmenovatel2 := collect(% / coeff(%, z, 0), z); |
| > |
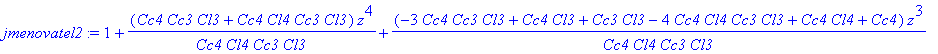
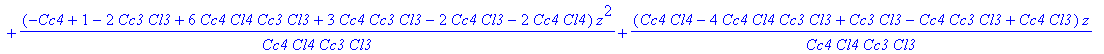
Jmenovatel funkce, kterou chceme touto sekcí realizovat
| > | Hdd2; |
| > |
Porovnání koeficientů - nalezení hodnot součástek
| > | hodnoty2 := solve({ coeff(jmenovatel2, z, 4) = coeff(Hdd2, z, 4), coeff(jmenovatel2, z, 3) = coeff(Hdd2, z, 3), coeff(jmenovatel2, z, 2) = coeff(Hdd2, z, 2), coeff(jmenovatel2, z, 1) = coeff(Hdd2, z, 1) }, {Cc4, Cl4, Cl3, Cc3}); |
| > |
Celý obvod (obě sekce) s vypočtenými hodnotami součástek
| > | ####### |
| > |
| > | obvpp:=" |
| > | V1 1 0 1 AC S1 2 1 1 S2 2 4 2 S3 3 0 1 S4 3 5 2 S5 8 0 1 S6 8 6 2 S7 9 0 1 S8 9 5 2 S9 10 0 1 S10 10 5 2 S11 11 0 1 S12 11 7 2 S13 13 12 1 S14 13 0 2 S15 14 0 1 S16 14 7 2 S17 16 15 1 S18 16 0 2 S19 17 18 1 S20 17 7 2 S21 19 6 1 S22 19 0 2 S23 20 0 1 S24 20 21 2 S25 22 6 1 S26 22 24 2 S27 23 0 1 S28 23 25 2 S29 27 0 1 S30 27 26 2 S31 28 0 1 S32 28 25 2 S33 31 30 1 S34 31 0 2 S35 32 0 1 S36 32 29 2 S37 34 33 1 S38 34 0 2 S39 35 36 1 S40 35 29 2 S41 37 26 1 S42 37 0 2 S43 38 33 1 S44 38 0 2 S45 39 26 1 S46 39 0 2 S47 40 0 1 S48 40 41 2 A1 7 0 0 5 A2 4 0 0 12 A3 6 0 0 15 A4 18 0 0 21 A5 29 0 0 25 A6 24 0 0 30 A7 26 0 0 33 A8 36 0 0 41 Cu1 2 3 1 Cu2 8 9 1 Cu3 13 14 1 Cu4 16 17 1 Cu5 19 20 1 Cs 10 11 1 Cc1 5 7 2.113932413 Cl1 4 12 .6003879223 Cl2 6 15 5.679468038 Cc2 21 18 .2197135404 Cu6 22 23 1 Cu7 27 28 1 Cu8 31 32 1 Cu9 34 35 1 Cu10 39 40 1 Cl 37 38 1 Cc3 25 29 11.80777718 Cl3 24 30 .4873219825 Cl4 26 33 4.223958058 Cc4 41 36 .9673743961 .end": |
| > |
| > |
| > | vysledky := PraCAn(obvpp, TF, P = 2, SCIDEAL): prenos := eval(v("26")[1] / v("1")[1], vysledky); |
| > |
| > | prenosf := eval(prenos, {z = exp(I*2*Pi*f * T)}); |
| > |
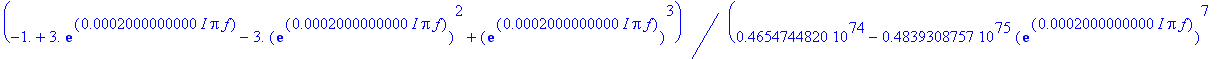
Přenos filtru - tvar charakteristiky je správný, ale bude ještě nutno pořešit vertikální posun.
| > | plot(20*log10(abs(prenosf)), f = 0..5000); |
![[Maple Plot]](images/pp577.gif)
Zjistíme potřebné zesílení z hodnoty maxima grafu (které se nachází např. na frekvenci 1198.5 Hz)
| > | potrebneZesileni := 1 / evalf(abs(eval(prenos, {z = exp(I*2*Pi*1198.5 * T)}))); |
| > |
Nejrůznějšími analýzami se nám podařilo zjistit, že je možné celkové zesílení dané sekce nastavit hodnotou vstupního kapacitoru (tedy mezi svorkami 2-3, resp. 22-23) a stejným číslem pak vynásobit hodnotu kapacitoru u druhého OZ v sekci (tedy mezi svorkami 4-12, resp. 24-30). Označme tato zesílení jako Au1 a Au2.
| > |
Poznámka k hodnotám součástek: při praktické realizaci můžeme hodnoty všech kapacitorů vynásobit zvolenou konstantou, přenosová funkce se tím nezmění a zajistíme tak realizovatelné hodnoty součástek.
| > | ####### |
| > |
| > | obvpp:=" |
| > | V1 1 0 1 AC S1 2 1 1 S2 2 4 2 S3 3 0 1 S4 3 5 2 S5 8 0 1 S6 8 6 2 S7 9 0 1 S8 9 5 2 S9 10 0 1 S10 10 5 2 S11 11 0 1 S12 11 7 2 S13 13 12 1 S14 13 0 2 S15 14 0 1 S16 14 7 2 S17 16 15 1 S18 16 0 2 S19 17 18 1 S20 17 7 2 S21 19 6 1 S22 19 0 2 S23 20 0 1 S24 20 21 2 S25 22 6 1 S26 22 24 2 S27 23 0 1 S28 23 25 2 S29 27 0 1 S30 27 26 2 S31 28 0 1 S32 28 25 2 S33 31 30 1 S34 31 0 2 S35 32 0 1 S36 32 29 2 S37 34 33 1 S38 34 0 2 S39 35 36 1 S40 35 29 2 S41 37 26 1 S42 37 0 2 S43 38 33 1 S44 38 0 2 S45 39 26 1 S46 39 0 2 S47 40 0 1 S48 40 41 2 A1 7 0 0 5 A2 4 0 0 12 A3 6 0 0 15 A4 18 0 0 21 A5 29 0 0 25 A6 24 0 0 30 A7 26 0 0 33 A8 36 0 0 41 Cu1 2 3 1*Au1 Cu2 8 9 1 Cu3 13 14 1 Cu4 16 17 1 Cu5 19 20 1 Cs 10 11 1 Cc1 5 7 2.113932413 Cl1 4 12 .6003879223*Au1 Cl2 6 15 5.679468038 Cc2 21 18 .2197135404 Cu6 22 23 1*Au2 Cu7 27 28 1 Cu8 31 32 1 Cu9 34 35 1 Cu10 39 40 1 Cl 37 38 1 Cc3 25 29 11.80777718 Cl3 24 30 .4873219825*Au2 Cl4 26 33 4.223958058 Cc4 41 36 .9673743961 .end": |
| > |
| > |
| > | vysledky:=PraCAn(obvpp, TF, P = 2, SCIDEAL): prenos := eval(v("26")[1] / v("1")[1], vysledky); |
| > |
Potřebné zesílení známe, rozdělme ho tedy mezi obě sekce spravedlivě skrzevá odmocninu.
| > | prenosf := eval(prenos, {z = exp(I*2*Pi*f * T), Au1 = sqrt(potrebneZesileni), Au2 = sqrt(potrebneZesileni)}); |
| > |
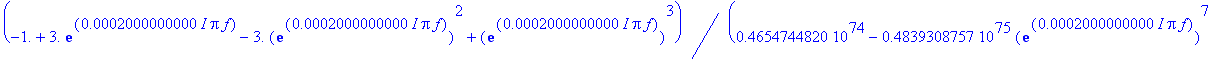
Správná charakteristika
| > | plot(20*log10(abs(prenosf)), f = 0..5000); |
![[Maple Plot]](images/pp586.gif)
Logaritmická frekvenční osa, vidíme opakování spektra v důsledku spinací frekvence.
| > | plots[semilogplot](20*log10(abs(prenosf)), f = 100..10000); |
![[Maple Plot]](images/pp587.gif)
Detail propustného pásma
| > | plot(20*log10(abs(prenosf)), f = 618..1618); |
![[Maple Plot]](images/pp588.gif)
| > |
Na závěr ještě vyzkoušejme přeladit filtr - změníme spinací frekvenci na dvojnásobek.
| > | T := 1 / 20e3; |
| > | prenosf := eval(prenos, {z = exp(I*2*Pi*f * T), Au1 = sqrt(potrebneZesileni), Au2 = sqrt(potrebneZesileni)}): |
| > | plots[semilogplot](20*log10(abs(prenosf)), f = 100..10000); |
![[Maple Plot]](images/pp590.gif)
| > |
| > |
Konec dobrý - všechno dobré.
| > |